[コンプリート！] 等差数列の和 公式 覚え方 286814-等差数列の和 公式 覚え方

 ここで図の赤枠で示している部分に注目してください。この部分は等差数列になっています。ですので、等差数列の 番までの和の公式を使って求めることができます。 そして出てきた値に初項を足すと 1＋45＝46となります。 答え46 まとめ公比の意味、等差数列との違いも併せて勉強しましょう。下記が参考になります。 等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 公差とは？1分でわかる意味、一般項、n項、等差数列との関係 管理人おすすめ！セットで3割もお得！等比数列、等差数列、公差の意味も併せて勉強しましょう。下記が参考になります。 等比数列の一般項は？1分でわかる求め方、和の計算、等差数列との違い 等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 公差とは？

規則性の問題を間違えないコツ 等差数列

等差数列の和 公式 覚え方

等差数列の和 公式 覚え方- 次が等差数列の和の公式です。 初項 a ，末項 l ，項数 n の等差数列の和 S = 1 2 n ( a l) 項 数 初 項 末 項 1 2 × ( 項数) × ( 初項 末項) 等差数列の和は 公式を言葉で覚えて 「 初項 」「 末項 」「 項数 」から求めている意識が重要です。 ちなみに，教科書には 1 2 n { 2 a ( n − 1) d } という公式があるけど，使うことはないので覚えなくていいです。 むしろ，考え陈金跃 等差数列求和公式的变换与意义j 中学数学研究, 02(12)4142 3 刘锡凤 等差数列求和公式的应用教学设计j 中国科教创新导刊, 13(2)9495 4 齐龙新, 王红艳 等差数列求和公式变式的灵活应用j 高中数理化, 09(2) 5 杜莹梅 等差数列求和公式的

数学b 等差数列 数列の和の公式と求め方がわかりやすい話 都立高校受験応援ブログ

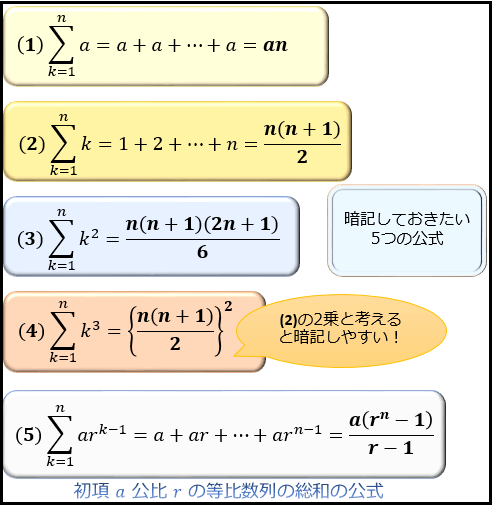
 等差数列・等比数列を分かりやすく考えるコツ 数列の和を求めるとき、式変形をするたびに毎回数列をすべて書いていたら、スペースがいくらあっても足りません。 そのため、多くの場合は総和記号 Σ （シグマ）を使ってまとめて計算することになります。 Σ の式は、k に 「k = 1,2,3,,n1,n」をそれぞれ代入した n 個の数列の合計 を意味する式です。 Σ を使った（ ）内は第1項から第（n1)項までの和である。これをΣ記号を使って表すと Σの計算の仕方 Σの計算の仕方は後ろに来る文字の次数によって公式がありましたね。 一応確認しておきましょう。 例題をやってみよう 次の数列｛αⁿ｝の一般項を求めましょう。等差数列 例： 2 4 6 ⋯ 100 = 2550 246\cdots 100=2550 2 4 6 ⋯ 100 = 2550 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16

計算例 / 数学公式集 / 数列の和; 等差数列の和はそれ自体は公式を覚えることで簡単に用いることができるのですが、応用させた問題が出題されることが多いので正しく理解することが必要です。 公式は以下の通りです。 簡単に証明してみます。 等差数列の和を\(S_n\)とします。 これを\(a_n\)で表すと \begin{align} 覚えなくていい「等比数列の和」 等差数列のときと似たような導入でかきます。 覚えなくていい「等差数列の和」 算数は得意なのに数学が苦手なひとのためのブログ まず、 等比数列 の公式として、 ( ∑nk = 1ak) = an 1 − a a − 1 こんな感じで教わってるかな？ それとも ( ∑nk = 0ak) = an 1 − 1 a − 1 みたいな感じ？

等差数列（とうさすうれつ）の一般項を求める公式は「an=a (n－1)d」です。 また、等差数列の和の公式はn (aan)/2で算定されます。 anはn番目の項、dは公差、aは初項です。 公差とは等差数列における一定の数dです。 今回は等差数列の公式、覚え方、等差数列の和の計算について説明します。 公差の意味は下記が参考になります。 公差とは？ 1分でわかる意味数学切り抜き帳 等差数列の和というと，初項 a ，公差 d ，項数 n である等差数列の和の公式 がよく使われるが，教科書や参考書には次の公式も書いてある． 等差数列の和 初項 a ，末項 l ，項数 n である等差数列の和 Sn は， この公式は，「台形の面積 等差数列の和を求める公式 等差数列の初項からある項までをすべて足し合わせる公式がある。 初項a、末項l、項数nの等差数列の和S n を求める公式は以下。 この公式についても具体的な数列を使いながら証明していきたい。 ＜公式の証明＞

1

等差数列の一般項と和 おいしい数学

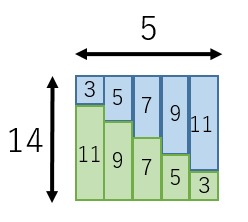
ここで，初項 3，公差 2，項数 10 の等差数列 3，5，7，9，11，13，15，17，19，21 を考え，その和を求めてみましょう。皆さんはどのようにして求めますか？ いろいろな求め方がありますが，ここでは，次のようにして求めることにします。 今，求める和を s前回 https//googl/LFNGHA 次回 https//googl/O1NiMG動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が解き方 解答 ， ， ， ， 第 項 ＝ 初項 ，公差 ，項数 の等差数列の和 求める数列の和は ， ， ， ， よって 4 まとめ Σシグマは苦手な人が多い分野なので、公式と解法をしっかり覚えて周りと差をつけよう。 この単元の「数列」の公式を、PDFファイルでプリント1枚にまとめました。 ダウンロードは こちら 数学B

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

規則性の問題を間違えないコツ 等差数列

 これが、等差数列の和には使えます。 等差数列で、初項からn番目までの項を すべて足した数の和は、 (初項n番目の項)×(項の数n)/2になります。 さきほどの、 (101×100) /2つまり(1001)×100/2 と比べると分かるはずです。 ここで、 最初の項がa、交差dとすると、 こんにちは。 da Vinch (@mathsouko_vinch)です。 等比数列の和等差数列でもやったように等比数列でもある任意の項までの和を考えてみます。少しトリッキーなことをするので最初はちょっとビックリするかもしれませんが、しっ等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算 等比数列の一般項は？1分でわかる求め方、和の計算、等差数列との違い 数列の例 数列の例を下記に示します。それぞれ等差数列、等比数列のどちらに該当するか考えてみましょう。

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

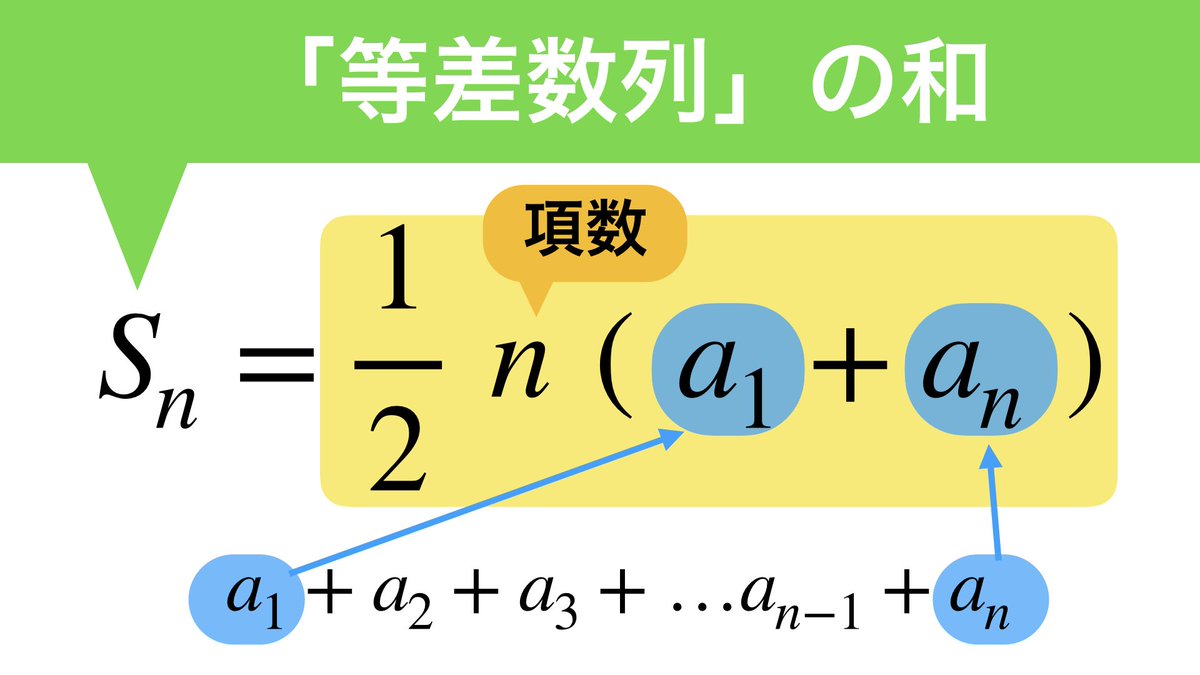
等差数列の和の求め方 ここでは，等差数列の初項 から第 項までの和 を求めてみよう． STEP1 等差数列の一般項 に， を代入して足し合わせる式を書く． STEP2 この式の右辺を，逆に並べて書く． STEP3 上の2式を縦に足し合わせる． 右辺は全て であり 数列の和とΣ (シグマ)記号の意味と使い方 ＊この記事では、 等差数列の一般項 と 等比数列の一般項 は既知として、Σ公式やその証明などを解説していきます。 もし、分からなければ先に→ 等差数列と等比数列の一般項（漸化式の解き方） をぜひ読んこの問題は、 「等差数列の和の公式」 を覚えていないと解くのが難しいのです。 等差数列の和の公式は、 N番目までの等差数列の和＝｛初項（初めの数）＋末項（終わりの数）｝×項数（個数）÷2

等差数列の和を計算する2つの公式 具体例で学ぶ数学

数学ｂ 等差数列の和の求め方とコツ 教科書より詳しい高校数学

 2 等比数列とは「同じ数をかけ続ける数列」 21 等比数列の定義を説明！ 22 「初項」「公比」だけを押さえれば一般項は求められる 3 等比数列の和の公式 31 和の公式を証明！ 32 和の公式が出てくる問題で練習しよう 4 大学入試でよく出る応用問題 41よって、初項＋公差× (n1)　これが等差数列の一般項を求める公式になります。 例えば先ほどの数列で番目の数はというと、3＋2× (1)=41となります。 まとめると、初項をa、公差をd、nを自然数とおいて、an=a (n−1)d　となります。

4年 5年 6年 算数 規則性 ラップde算数 歌で覚える等差数列の和の公式 無料でオンライン 受験ドクター Youtube

等比数列の一般項と和 おいしい数学

3

高校数学ｂ S公式 問題一覧 公式 覚え方 計算方法 学校よりわかりやすいサイト

等差数列 公式を導いてみよう N番目の数も和も簡単に求められる ページ 2 みみずく戦略室

数列の公式の簡単な覚えかたってありますか 等比 等差数列の一般項の公式 Yahoo 知恵袋

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

高校数学 見るだけ公式集 على تويتر 数学b イメージで覚える 等差数列の和 見るだけ数学 ビジュアルで覚えよう 高校生応援

これでわかる 数列のシグマsの計算方法を徹底解説

数学の質問です 写真のsの数列の和の公式が とても複雑でやや Yahoo 知恵袋

等差数列の和の公式の証明を超分かりやすく解説するよ

高校数学b 群数列の究極の2パターン 受験の月

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

等差数列の和の公式の例題と証明など 高校数学の美しい物語

等差数列を徹底解説 一般項の求め方や和の公式をマスターしよう Studyplus スタディプラス

等差数列の和の公式で 写真のような公式があると思いますが これの Yahoo 知恵袋

等差数列を徹底解説 一般項の求め方や和の公式をマスターしよう Studyplus スタディプラス

2

数学の質問です 等差数列の和の公式二つ 写真で色ペンで線が引いてあるもの Yahoo 知恵袋

等差数列の公式は覚えずに 自分で15秒で作ろう

1乗和 2乗和 3乗和の公式 導出法から理解しよう

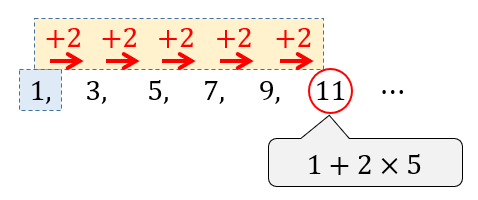
等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

階差数列の和 三角数 父ちゃんが教えたるっ

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

数学b 等差数列 数列の和の公式と求め方がわかりやすい話 都立高校受験応援ブログ

等差数列の一般項や和の公式をマスターしよう ますますmathが好きになる 魔法の数学ノート

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

基本 等差数列の和の公式 初項と公差 数列1 11 Youtube

数学b 等差数列 数列の和の公式と求め方がわかりやすい話 都立高校受験応援ブログ

等差数列の和の公式の証明を超分かりやすく解説するよ

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

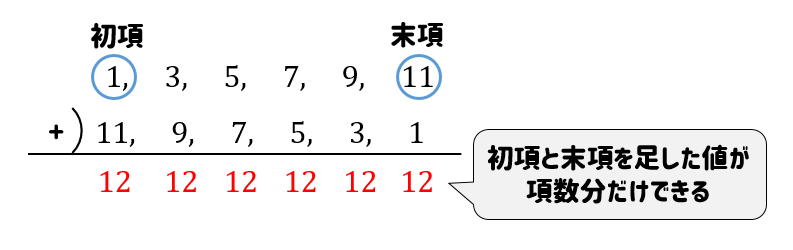
等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

等差数列の問題の解き方は 植木算や倍数の問題にも応用してみよう 中学受験ナビ

階差数列

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

等比数列の一般項と和 おいしい数学

数学b 等差数列 数列の和の公式と求め方がわかりやすい話 都立高校受験応援ブログ

等差数列の和の公式で 写真のような公式があると思いますが これの Yahoo 知恵袋

数学検定1級合格者が解説 等差数列の和 一瞬で覚える語呂合わせ 公式を覚えよう 数検 Youtube

2

1

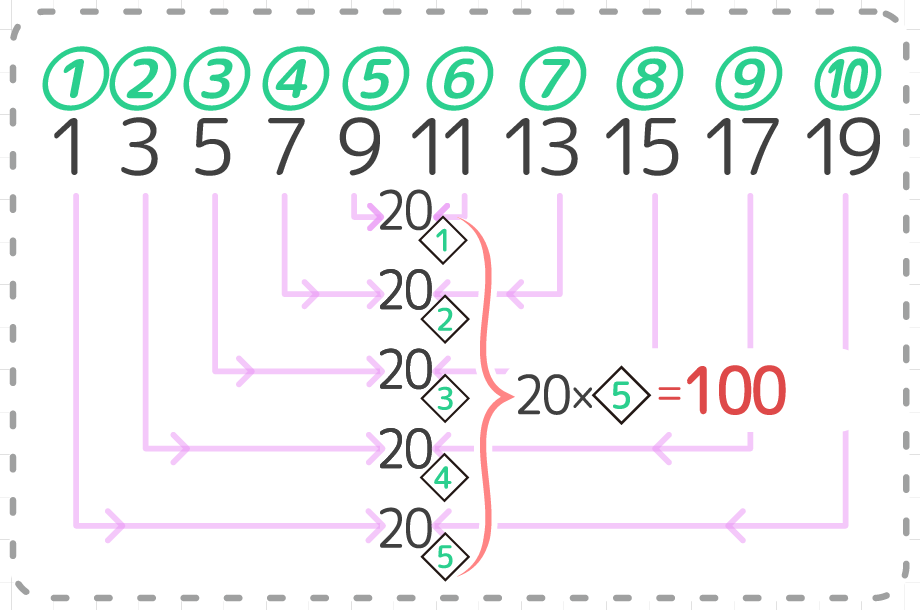
無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

1

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列５ 等差数列の和の公式は不要 ３ 怜悧玲瓏 高校数学を天空から俯瞰する

等比数列の和の公式の覚え方とは 問題を通してわかりやすく証明 極限についても考察 遊ぶ数学

５分間studying 数列 3 等差数列の和 数 Bを ぶっ飛ばせ

等差数列の和の公式の証明を超分かりやすく解説するよ

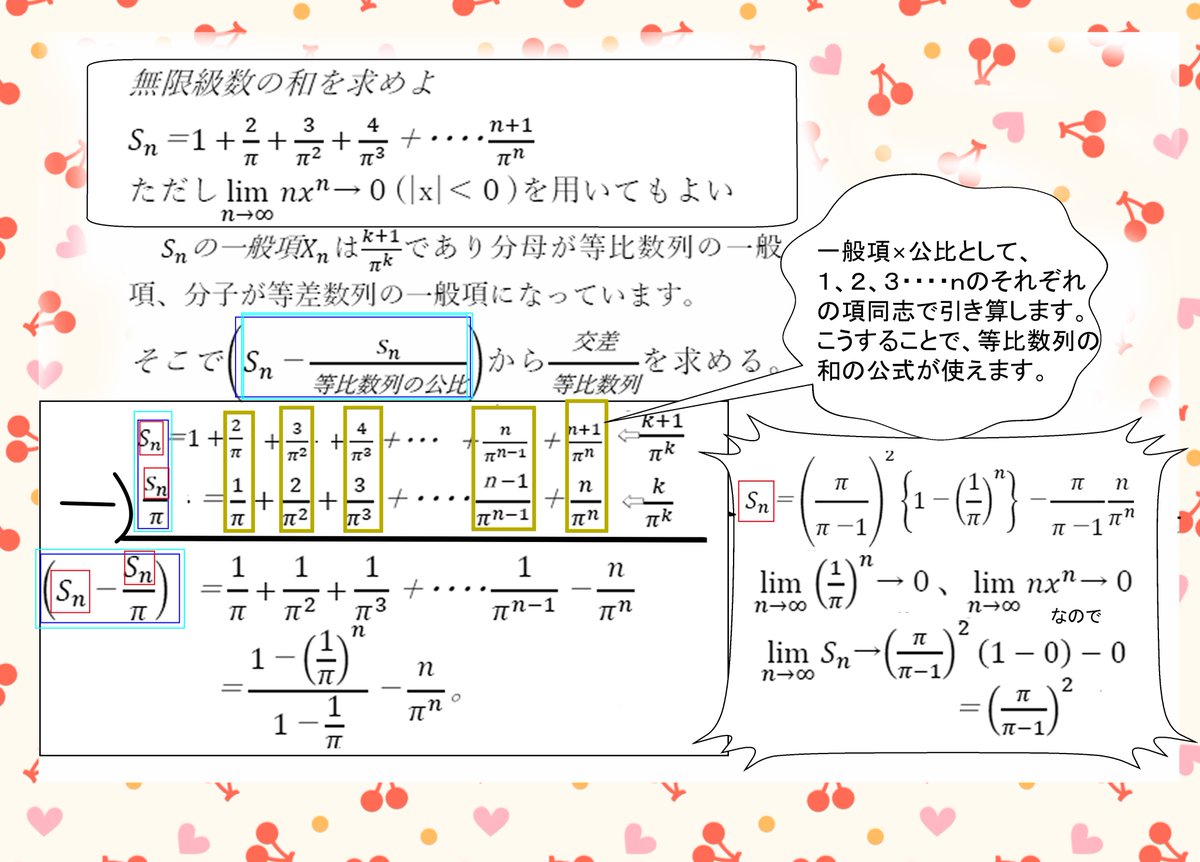
等差数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

等差数列の公式は覚えずに 自分で15秒で作ろう

等差数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

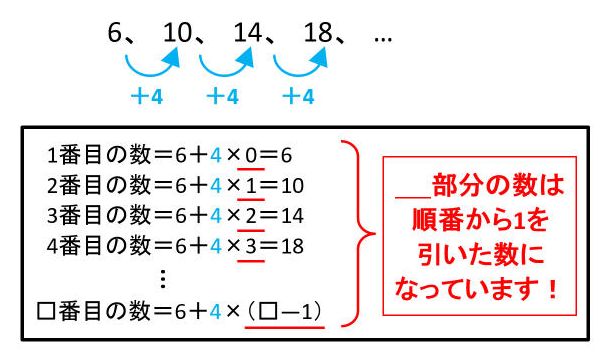
等差数列の問題の解き方は 植木算や倍数の問題にも応用してみよう 中学受験ナビ

等差数列の一般項と和 おいしい数学

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

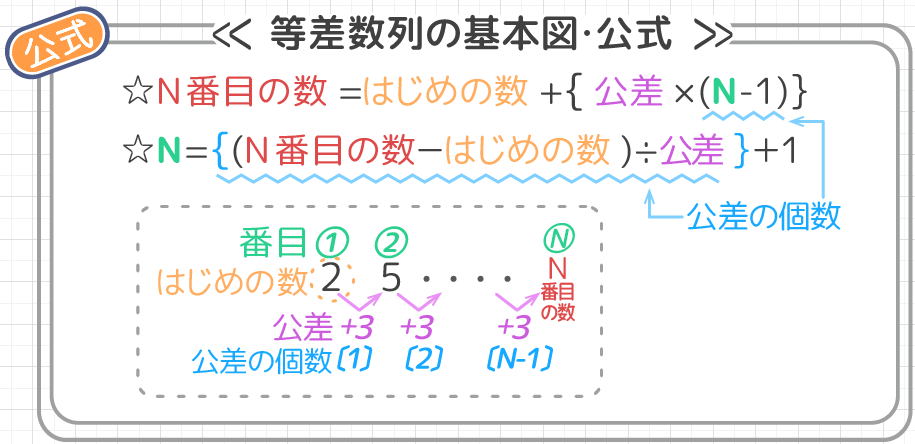
無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

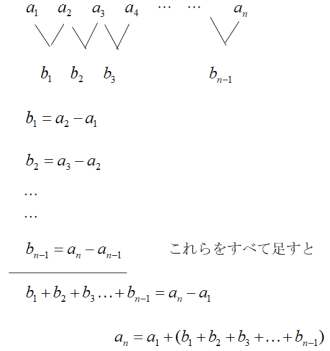
階差数列の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

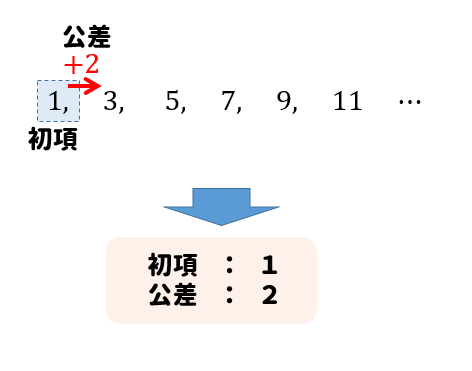
等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

覚えなくていい 等比数列の和 東大生の高校数学ブログ

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

階差数列を使った数列問題の解き方 公式を東大生がわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列の一般項と和 おいしい数学

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

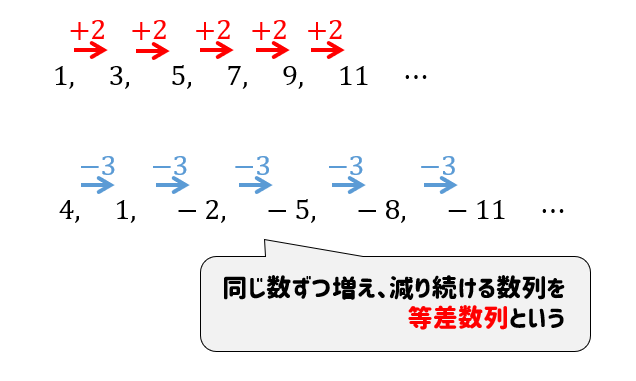
等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

高校数学b 等差数列 A N の一般項 １ 映像授業のtry It トライイット

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数学検定1級合格者が解説 等差数列の一般項 一瞬で覚える語呂合わせ 公式を覚えよう 数検 Youtube

等比数列の一般項と和 おいしい数学

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

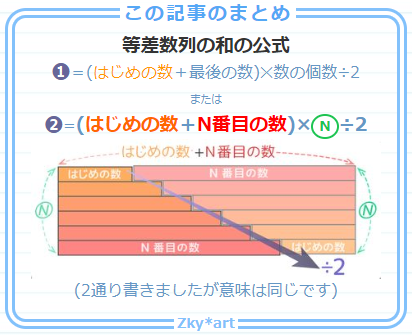
無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

高校 数学b 数列５ 等差数列の和１ １６分 Youtube

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

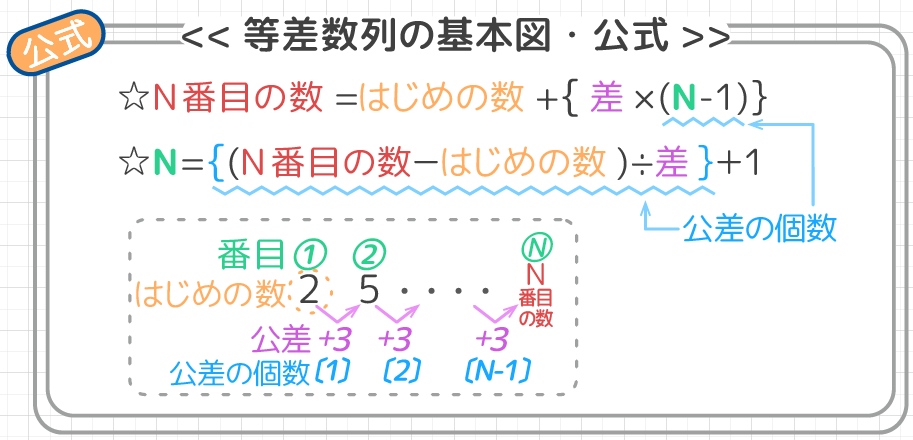
中学受験 等差 数列とは 問題と解き方まとめ 無料プリントも 小学生 そうちゃ式 受験算数 新1号館

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

階差数列

規則性 数列の基本 中学受験準備のための学習ドリル

5分で分かる 等差数列の和の公式は覚えなくていいです 一番簡単な方法を教えます Youtube

Incoming Term: 等差数列の和 公式 覚え方,